ANSWERS to Ch. 9 Review Problems

9.1 #4 D(25,-π/4); E(15,π/2); F(20,π/12) #6 see below; triangle #46 (3,π/2); (5,0); (√(5),arctan(2)) ≈ (2.236,1.107) #50 (3,0); (0,5); (-1,0)

9.2 #10 see below (a) θ = π/6, θ = 5π/6 (b) θ = π/2, θ = 7π/6, θ = 3π/2, θ = 11π/6 (c) θ = π/2, θ = 3π/2 (d) θ = π/2

#14 `4^2 - int_0^(2pi) (1/2) (1+sin(theta))^2 \ d theta = 16 - (3pi)/(2) approx 11.2876` #16 `int_(pi/2)^(pi) (1/2)[(theta^2)^2 - (theta)^2] \ d theta approx 25.1239` #18 (a) `int_0^(2pi) (1/2) (1.5+cos(2theta))^2 \ d theta approx 8.639` (b) `int_0^(2pi) (1/2) (a+cos(2theta))^2 \ d theta`

#24 `int_(2pi)^(4pi) sqrt((theta)^2 + 1) \ d theta = approx 59.563` #28 `int_(0)^(2pi) sqrt((1.2+cos(theta))^2 + (-sin(theta))^2) \ d theta = approx 8.92`

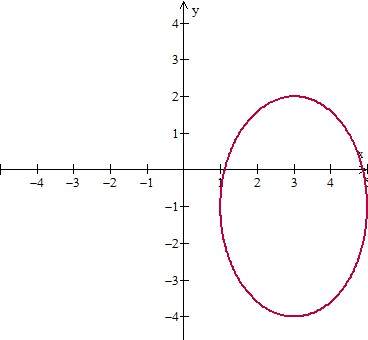
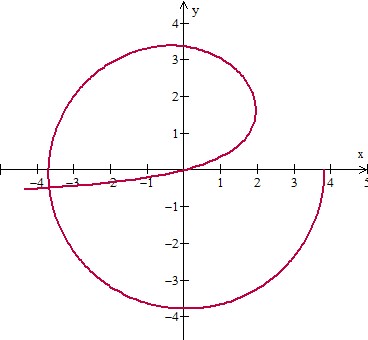
9.3 #12 see below; ellipse #16 see below

9.4 #8 (a) see below (b) 1; 2e; 5e² (c) nowhere #12 (a) 1; 1; 1; 1 (b) nowhere #14 1; 2√(5); √(185) #24 (a) `int_0^2 sqrt((3t^2+1)^2 + (2t)^2) \ dt` (b) 10.8 #30 `int_0^(pi/2) (2+sin(t)) \ cos(t) \ dt` (b) 2.5

9.5 #18 2x² + 10xy - 2y² - 7x + 3 = 0; 116; hyperbola

9.6 #14 e = 37; ellipse; (16/17,0), (0,0.8335),  (-16/11,0), (0,-1.817)